|
Articles 46,830
간단할 줄 알았는데 겁나 어렵네요..
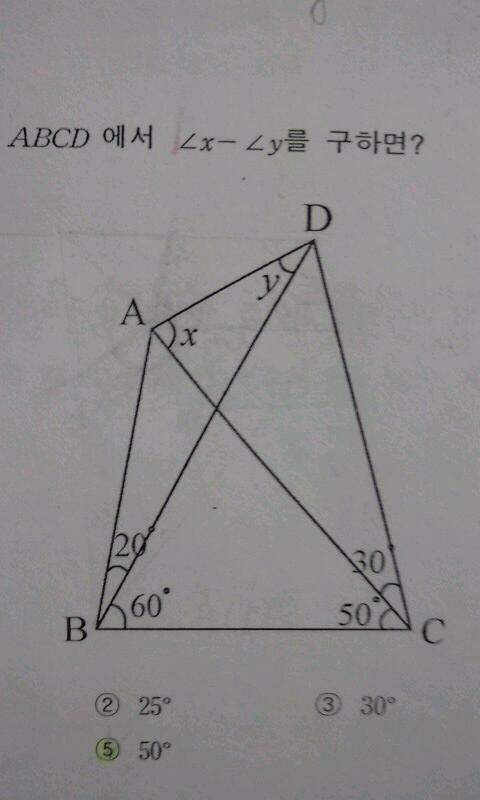
먼저 '삼각형의 내각의 합은 180도임' 요 공식을 이용합니다.
도형의 가운데 점을 O라고 하고, 삼각형 BOC에 위 공식을 적용하여
각 BOC는 110도 임을 찾아냅니다.
고로 반대편의 각 AOD도 110도 임을 알아낼 수 있겠죠.
삼각형 AOD에 윗 공식을 다시 적용하면 x+y=110도 임을 찾아낼 수 있습니다.
요기까지가 조건 1...
그 담에 선분 CD위에 한 점 K를 잡습니다. 이때 각CBK가 20도가 되게끔요..
고렇게 잡고 선분을 그려 삼각형 CBK를 만들고 나면
요게 '이등변 삼각형이다' 라는걸 알 수 있습니다.
(왜냐면요 맨첨 각 20도로 잡았고 원래 각 BCD는 80도라서
내각의 합은 180도임 공식을 이용하면 반대편 각도 80도임을 알 수 있죠.
양쪽의 각이 같으니 이등변 삼각형입니당..)
암튼 이등변 삼각형이기 때문에 선분 BC와 BK..는 길이가 같음을 알 수 있습니다.
여기서 삼각형 ABC를 보시면 또 이등변 삼각형임을 알 수 있습니다.
(각 BAC=BCA) 고로 선분 BC=BK=BA임을 알 수 있는데요, 여기서 잘 보면
선분 BA=BK인데 사잇각이 60도에요.. 즉 삼각형 ABK는 정삼각형입니다.
고로 선분 BC=BK=BA=AK...각 BKA는 60도가 되고
맨첨에 그렸던 이등변 삼각형 CBK의 한쪽 각이 80도라서 각 AKD는 40도가 됨을 알 수 있습니다.
(각 BKA + CKB + AKD = 180 이어야 하므로...)
그런데 여기서 또 잘 보면 각 삼각형 KBD는 이등변 삼각형임을 알 수 있습니다.
(각 KBD는 60-20해서 40도, 각 BKD는 60+40해서 100도, 내각의 합은 180이므로
나머지 한각이 40도.. 고로 양 각이 같으므로 이등변 삼각형)
따라서 각 KDB도 40도가 되고 선분 BC=BK=BA=KD=KA 임을 알 수 있습니다.
오호라 여기서 삼각형 AKD를 보니 각 AKD는 40도로 공유하고
양 변의 길이가 같으므로 이등변 삼각형이겠네요 ^-^
따라서 (y+40)*2 + 40 = 180 (삼각형 내각공식..)
계산하면 y=30 !! 요게 두번째 조건입니당
첫 번째 조건에 두 번째 조건을 대입하면 x=80이 나오는군여..
고로 x-y = 50!!
중학교 졸업한지 오래되서 그런지.. 직관적인 방법밖에 생각이 안나네요
더 쉬운 방법이 분명 있었던거 같은데...
먼저 '삼각형의 내각의 합은 180도임' 요 공식을 이용합니다.
도형의 가운데 점을 O라고 하고, 삼각형 BOC에 위 공식을 적용하여
각 BOC는 110도 임을 찾아냅니다.
고로 반대편의 각 AOD도 110도 임을 알아낼 수 있겠죠.
삼각형 AOD에 윗 공식을 다시 적용하면 x+y=110도 임을 찾아낼 수 있습니다.
요기까지가 조건 1...
그 담에 선분 CD위에 한 점 K를 잡습니다. 이때 각CBK가 20도가 되게끔요..
고렇게 잡고 선분을 그려 삼각형 CBK를 만들고 나면
요게 '이등변 삼각형이다' 라는걸 알 수 있습니다.
(왜냐면요 맨첨 각 20도로 잡았고 원래 각 BCD는 80도라서
내각의 합은 180도임 공식을 이용하면 반대편 각도 80도임을 알 수 있죠.
양쪽의 각이 같으니 이등변 삼각형입니당..)
암튼 이등변 삼각형이기 때문에 선분 BC와 BK..는 길이가 같음을 알 수 있습니다.
여기서 삼각형 ABC를 보시면 또 이등변 삼각형임을 알 수 있습니다.
(각 BAC=BCA) 고로 선분 BC=BK=BA임을 알 수 있는데요, 여기서 잘 보면
선분 BA=BK인데 사잇각이 60도에요.. 즉 삼각형 ABK는 정삼각형입니다.
고로 선분 BC=BK=BA=AK...각 BKA는 60도가 되고
맨첨에 그렸던 이등변 삼각형 CBK의 한쪽 각이 80도라서 각 AKD는 40도가 됨을 알 수 있습니다.
(각 BKA + CKB + AKD = 180 이어야 하므로...)
그런데 여기서 또 잘 보면 각 삼각형 KBD는 이등변 삼각형임을 알 수 있습니다.
(각 KBD는 60-20해서 40도, 각 BKD는 60+40해서 100도, 내각의 합은 180이므로
나머지 한각이 40도.. 고로 양 각이 같으므로 이등변 삼각형)
따라서 각 KDB도 40도가 되고 선분 BC=BK=BA=KD=KA 임을 알 수 있습니다.
오호라 여기서 삼각형 AKD를 보니 각 AKD는 40도로 공유하고
양 변의 길이가 같으므로 이등변 삼각형이겠네요 ^-^
따라서 (y+40)*2 + 40 = 180 (삼각형 내각공식..)
계산하면 y=30 !! 요게 두번째 조건입니당
첫 번째 조건에 두 번째 조건을 대입하면 x=80이 나오는군여..
고로 x-y = 50!!
중학교 졸업한지 오래되서 그런지.. 직관적인 방법밖에 생각이 안나네요
더 쉬운 방법이 분명 있었던거 같은데...